Abychom si nejdříve objasnili pojem funkce, uvedeme zjednodušenou definici funkce jedné proměnné a na příkladech si ji objasníme.
Funkce je předpis, který každému \(x\) přiřazuje právě jedno \(y\).
Proměnné \(x\) se říká nezávisle proměnná, protože ji volíme libovolně. Naproti tomu proměnné \(y\) se říká závisle proměnná, protože její hodnota je závislá na námi zvolené proměnné \(x\). Pojďme si definici objasnit na příkladu.
Příklad 1
Uvažujme funkci \(y=2x+4\). Společně zjistěme funkční hodnoty v námi libovolně zvolených bodech.
Poznámka: Často se používá i ekvivalentní zápis \(f(x)=2x+4\). Označení \(f(x)\) má tu výhodu, že je ze zápisu jasně vidět, na jaké proměnné je funkce závislá. Zápis \(f(x)\) nám říká, že funkce \(f\) je závislá na proměnné \(x\). Analogicky, zápis \(f(\alpha, \beta)\) označuje funkci závislou na dvou proměnných – proměnné \(\alpha\) a proměnné \(\beta\).
Řešení 1
Pro ty z nás, kteří se s funkcemi doposud nikdy nesetkali, rozebereme tento příklad podrobně. O pár řádků výše jsme si prozradili, že hodnoty \(y\) jsou závislé na námi libovolně zvolených \(x\). Pár libovolných \(x\) si tedy zkusíme dosadit. Pro přehlednost si pomůžeme tabulkou.
Z tabulky vidíme, že pokud do funkce \(y=2x+4\) dosadíme za \(x\) číslo \(-5\), dostaneme \(y=2*(-5)+4=-6\). Stejný postup použijeme i pro ostatní námi zvolená \(x\).
V zadání příkladu 1 jsme uvedli pojem funkční hodnota. Funkční hodnotou rozumíme hodnotu proměnné \(y\), kterou získáme po dosazení proměnné \(x\) (druhý řádek tabulky jsou tedy funkční hodnoty pro námi zvolená \(x\)). Pokud si položíme otázku, jaká je funkční hodnota v bodě \(x=2\), odpovíme, že funkční hodnota v bodě \(x=2\) je \(8\) a matematicky zapíšeme \(f(2)=8\). Analogicky \(f(-1)=2\) znamená, že funkční hodnota v bodě \(x=-1\) se rovná \(2\).
Zkuste si pro trénink sami zapsat i ostatní funkční hodnoty.
Příklad 2
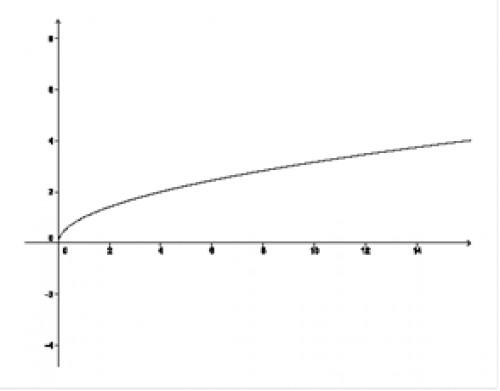
Rozhodněte, která z daných křivek představuje graf funkce.
Pro vyřešení tohoto příkladu budeme potřebovat naší zjednodušenou definici. Funkce je předpis, který každému \(x\) přiřazuje právě jedno \(y\). Jinými slovy, pokud zvolíme libovolné \(x\), musí k němu existovat právě jedno \(y\).
Řešení 2
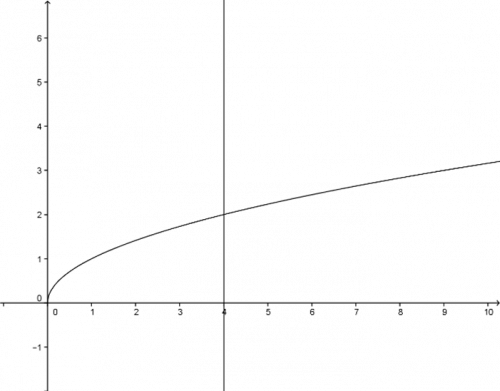
a) Zvolme například \(x=4\). Je krásně vidět, že přímka \(x=4\) protíná křivku právě v jednom bodě. Pro \(x=4\) tedy existuje právě jedno \(y\) a je zřejmé, že to samé bude platit pro všechna \(x\geq0\).
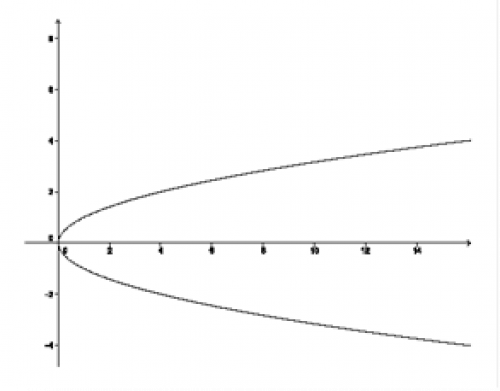
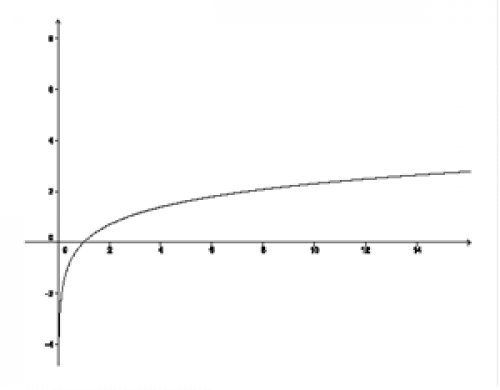
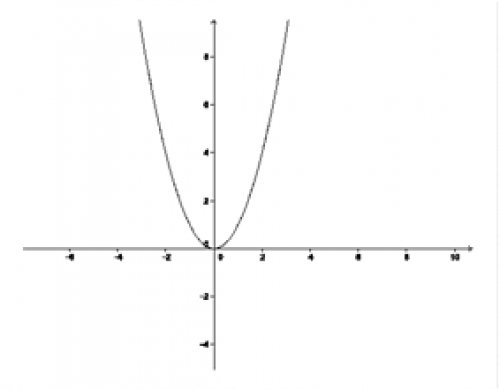
Řešení b), c), d)
Jedině křivka na obrázku b) není grafem funkce, protože pro všechna \(x>0\) protnou přímky křivku právě ve dvou bodech. Křivky na obrázcích c) a d) jsou grafy funkcí.
Nyní si pojďme definici funkce trochu rozšířit o definiční obor a obor hodnot.
Funkce je předpis, který každému číslu \(x\) z definičního oboru přiřazuje právě jedno \(y\) z oboru hodnot. Jak jsme již viděli, funkci lze obecně zapsat ve tvaru \(y=f(x)\), kde se zdůrazňuje, že \(y\) je funkce závislá na proměnné \(x\).