Obecný předpis kvadratické funkce vypadá takto: \(f(x)=ax^2+bx+c\), kde \(a\), \(b\), \(c\) jsou reálná čísla a platí, že \(a\neq0\). Stejně jako lineární funkce je vždy popsána přímkou, kvadratická funkce je zase vždy popsána parabolou.
Parabola má tvar písmene „U“, tedy kvadratická funkce je pokaždé omezená shora nebo zdola. Pojďme si uvést příklad.
Příklad 1
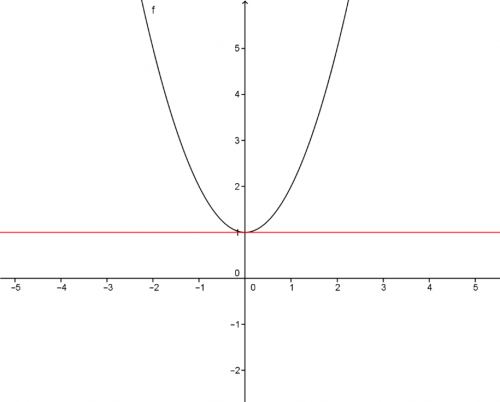
Na následujícím obrázku je znázorněný graf funkce \(f(x)=x^2+1\) a červeně osa \(y=1\). Jak můžeme vidět, osa \(y=1\) je limitní hranice, pod kterou se graf funkce nikdy nepodívá. Tudíž je omezen zdola.
\(f(x)=x^2+1\)
Tvar paraboly
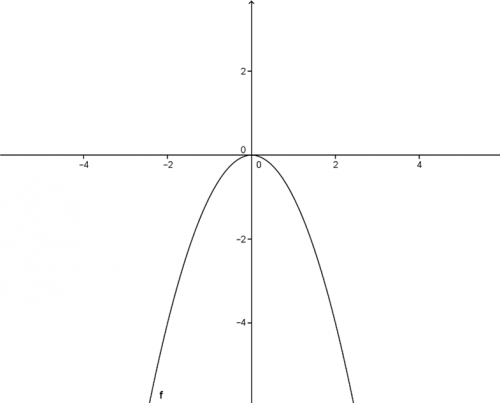
Koeficient \(a\) má zásadní vlil na tvar grafu kvadratické funkce. Jestliže je parametr \(a\) záporný, graf funkce bude překlopený přes osu x do záporných čísel.
\(f(x)=-x^2\)
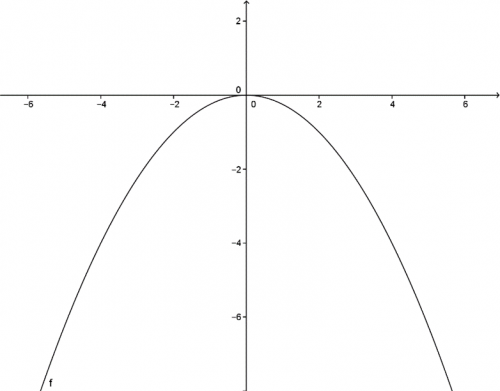
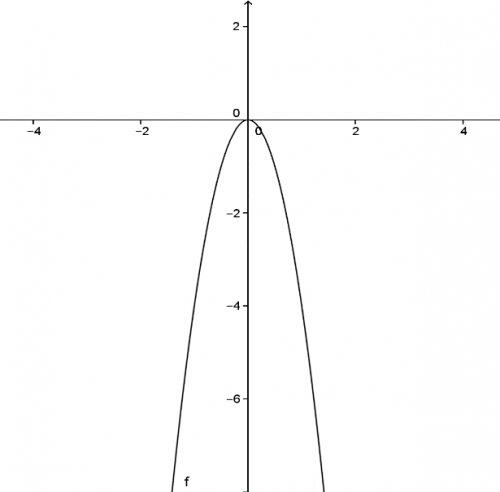
Pokud je koeficient \(a\) v absolutní hodnotě větší než jedna \((|a|>1)\), znamená to, že funkce bude zúžená k ose y. Je to podobné, jako u lineární funkce koeficient \(k\). Čím je toto číslo v absolutní hodnotě větší, tím rychleji funkce roste, resp. klesá. Podívejme se na dva příklady. Vlevo na obrázku vidíme funkci \(f(x)=4x^2\) a vpravo funkci \(g(x)={1\over 4}x^2\). Funkce \(g\) oproti \(f\) roste pomaleji.
Pojďme se nyní naučit graf kvadratické funkce načrtnout.
Příklad 2
\(y=(x-2)^2+3\)
K načrtnutí grafu kvadratické funkce musíme znát dvě věci. 1) Pokud se proměnná \(x\) vyskytuje v závorce ještě s dalším číslem, posouváme vrchol paraboly po ose x a to o hodnotu, po jejímž dosazení za \(x\) v závorce vychází nula. 2) Číslo stojící samostatně značí posunutí vrcholu paraboly po ose y a posouváme stejně jako u lineárních funkcí. Pojďme se tedy vrhnout na příklad 7.
Proměnná \(x\) má k sobě v závorce parťáka číslo \(-2\). Do jakého bodu na ose x posuneme vrchol paraboly? Do nulového bodu závorky. Hledaný bod je \(x=2\). Po dosazení dvojky za \(x\) se totiž celková hodnota závorky rovná nule. Kam posuneme vrchol paraboly ve směru osy y? Do \(y=3\). Posunutí po ose y nám udává hodnota stojící za závorkou samostatně. Nyní jsme schopni načrtnout graf.
Grafem kvadratické funkce je parabola. Bod \(A=[2;3]\) na obrázku značí vrchol paraboly. Abychom lépe porozuměli principu získání souřadnic vrcholu paraboly, uvedeme další příklady. Mějme přitom na paměti, že stejný způsob budeme používat i u ostatních typů funkcí.
Příklad 3
a) \(y=(x+2)^2-2\)
Při řešení hledáme nejdříve nulový bod závorky. Čemu se musí rovnat \(x\), aby v závorce vycházela nula? \(x=-2\). Vrchol paraboly tedy po ose x posuneme do bodu \(x=-2\). A posunutí po ose y? To je ještě jednodušší. Koukneme a vidíme, že po ose y posuneme vrchol paraboly také do \(-2\). Vrchol paraboly má tedy souřadnice \([-2;-2]\).
b) \(y=x^2+4\)
Pokud se člen \(x^2\) vyskytuje samostatně (není s parťákem uzavřený v závorce), k posunutí dochází pouze ve směru osy y. Vrchol paraboly má tedy souřadnice \([0;4]\).
c) \(y=-({x-{2\over 3}})^2-4\)
Nulový bod závorky je \(x={2\over 3}\). Po ose y posuneme vrchol paraboly o čtyři jednotky dolů. Vrchol paraboly má tedy souřadnice \([{2\over 3};-4]\). Podívejme se nyní ještě jednou na předpis funkce. Mínus před kvadratickým členem (jednoduše řečeno před závorkou) nám signalizuje, že je třeba graf funkce překlopit. Pro lepší porozumění uvedeme dva obrázky.
1) \(y={(x-{2\over 3})}^2-4\) 2) \(y=-({x-{2\over 3}})^2-4\)
Funkce na obrázku 1) a 2) se liší znaménkem před kvadratickým členem, a proto jsou jejich grafy zrcadlovými obrazy (graf na obrázku b) je stejný jako na obrázku a), pouze převrácený). Mějme na paměti, že mínus před nezávisle proměnou \(x\) signalizuje převrácení grafu i u ostatních typů funkcí. Ne pouze u kvadratické.